UNIDADE  III:    Campo elétrico

Região do espaço ao redor de uma carga elétrica Q onde manifestam-se  ações elétricas, isto é, se uma carga de prova q for colocada em um ponto P qualquer dessa região, ela fica sujeita a uma força de natureza elétrica. Dizemos então que nessa região do espaço existe campo elétrico.

Utilizaremos as seguintes denominações:

Q carga fonte ou carga geradora: carga que dá origem ao campo elétrico considerado

Q carga de prova ou carga teste: carga sobre a qual o campo elétrico está agindo.

O campo elétrico possui intensidade, direção e sentido, ou seja, é uma grandeza vetorial.

Vetor campo elétrico

Para representar a direção e o sentido do campo elétrico, usamos duas formas: o vetor  ou linhas orientadas, denominadas linhas de força.

Quando o campo elétrico for criado por cargas elétricas positivas, ele terá, por convenção, um sentido de afastamento.

Quando o campo elétrico for criado por cargas elétricas negativas, ele terá, por convenção, um sentido de aproximação.

O sentido do campo elétrico depende exclusivamente do sinal das cargas que o geram. Ele não depende da carga de prova.

Para determinar a existência de um campo elétrico, devemos colocar uma carga de prova eletrizada na região do espaço em que há um campo elétrico, dessa forma verificaremos que tal carga fica sujeita a uma força elétrica (F). Portanto, as fontes de campo elétrico são corpos eletrizados, que chamamos de cargas fonte (Q).

Ao mover uma carga elétrica de prova em um campo elétrico, ela ficará sujeita a diferentes intensidades de força elétrica. Em cada ponto do campo elétrico definimos um vetor campo elétrico (E). A intensidade desse campo elétrico é dada pela seguinte expressão: E= F/q

Na expressão acima, E é o vetor campo elétrico e F é o vetor força elétrica sobre a carga de prova (q), no ponto considerado. No Sistema Internacional de Unidades, a unidade para o campo elétrico é newton por coulomb (N/C). A partir da definição anterior, podemos escrever:

Os sentidos dos vetores E e F em relação a q:

Módulo do campo elétrico

Usando a definição de campo é possível demonstrar que num ponto P qualquer, o módulo campo elétrico, gerado por uma carga elétrica puntiforme Q, imersa no vácuo, é dado por:

Campo elétrico de várias cargas

Quando um campo elétrico é gerado por mais de uma carga elétrica, cada uma delas gera seu próprio campo, independente das demais. O campo elétrico será dado pela soma vetorial desses campos individuais.

                                                                                         

 

Exemplo:

Determinar a intensidade do vetor campo elétrico resultante no ponto P, nos casos a seguir. Considere o meio o vácuo:

a)                      4,0 m                 P         3,0 m

                                                                                                                                     Q₁= +16µC                                               Q₂= +9,0 µC

b)                       4,0 m                 P         3,0 m

                                                                                           

Q₁= +16µC                                               Q₂= -9,0 µC

 Linhas de força do campo elétrico de duas cargas puntiformes

Quando houver duas cargas puntiformes Q₁ e Q₂, gerando um mesmo campo elétrico, ocorrerá uma superposição de efeitos. Basicamente, cargas positivas geram campo de afastamento, onde “nascem” linhas de força, enquanto cargas negativas geram campo de aproximação, onde “morrem” linhas de força.

As linhas de força de um campo elétrico, além de darem uma idéia do aspecto geral do campo, podem ser utilizadas para se determinar a direção e o sentido deste num determinado ponto. Basta desenhar um vetor E   tangenciando a linha de força , acompanhando o seu sentido.

 

Campo elétrico de um condutor esférico

Em um condutor esférico eletrizado, a carga elétrica se distribui sempre na superfície externa do condutor, não havendo carga elétrica na parte interna, seja o condutor maciço ou oco.

O campo elétrico é nulo em qualquer ponto interno do condutor;

O campo elétrico nos pontos externos ao condutor é idêntico ao gerado por uma carga elétrica pontual, considerando a carga concentrada no centro do condutor;

Portanto, para calcular a intensidade do vetor campo elétrico  num ponto P externo, a fórmula é a mesma da carga pontual, sendo a distancia  d tomada a partir do centro da esfera.

Exemplo:

Uma esfera condutora de raio R= 40 cm está uniformemente eletrizada com carga Q=4,0 µC.

a)determine a intensidade do vetor campo elétrico num ponto P situado a 10 cm do centro da esfera;

b) )determine a intensidade do vetor campo elétrico num ponto P situado a 20 cm do centro da esfera;

c) )determine a intensidade do vetor campo elétrico num ponto P situado a 60 cm da superfície  da esfera.

Campo elétrico uniforme

Ele pode ser obtido eletrizando-se duas placas planas paralelas com cargas de sinais contrários e a pequena distancia uma da outra. A característica mais importante desse campo elétrico é que, em qualquer um de seus pontos, o vetor campo elétrico é sempre o mesmo, em direção, sentido e intensidade.

Exercicios:

UNIDADE II - DILATAÇÃO TÉRMICA

 2.1-Conceito:

 Como  já sabemos, se aumentarmos a temperatura de um corpo, aumentamos a agitação das partículas desse corpo. Consequentemente, as partículas se afastam umas das outras, provocando um aumento das dimensões (comprimento, área e volume) do corpo

  A esse aumento das dimensões do corpo dá-se o nome de Dilatação térmica.

  Se  a temperatura diminuir e as dimensões se reduzirem, dizemos que houve uma Contração Térmica.

  Embora o aumento ocorra em todas as dimensões do corpo simultaneamente costuma-se dividir o estudo da dilatação térmica em três partes:

·     Dilatação Linear: aquela que predomina o aumento em uma dimensão (comprimento).

         Ex.: dilatação em fios, cabos e barras

·        Dilatação Superficial: aquela que predomina o aumento em duas dimensões (área).

    Ex.: aumento em chapas e placas.

·        Dilatação volumétrica: é a dilatação em que se considera o aumento em três dimensões.

     Ex.: aumento de volume de um corpo.

   Os corpos sólidos admitem os três tipos de dilatação, mas os líquidos e gases, por não terem forma própria, só admitem a dilatação volumétrica.

2.2-Dilatação Linear

 Considere uma barra metálica de comprimento inicial Lo, à temperatura inicial To, ao aquecermos a barra até a temperatura T , seu comprimento aumentará para L.  
    

                                                                                             

   

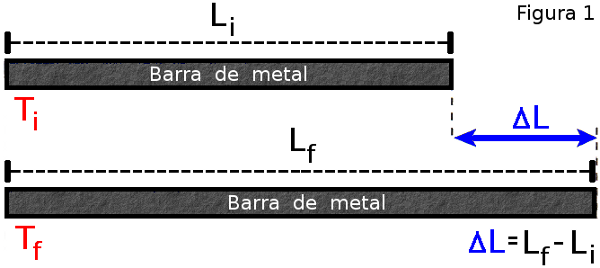
    DT = T_f - T_i: variação de temperatura

    DL = L_f - L_i: variação de comprimento

 Experimentalmente, verificou-se que a variação do comprimento  DL depende:

·     1º da variação de temperatura  DT: a variação do comprimento é diretamente proporcional a variação da temperatura.

                                    DL a     DT

·        2º do comprimento inicial Li: a variação do comprimento é diretamente proporcional ao comprimento inicial. 

                                    DL a   Li

 Utilizando-se barras de mesmo material, verificamos que a variação de comprimento depende somente destes dois fatores. Será  portanto proporcional ao produto deles.

                                 

                             DL  a   Li.   DT        DL = a. Li. DT

   

 A constante de proporcionalidade que aparece na equação, é uma característica do material da barra e é chamada coeficiente de dilatação linear. Há  pois, um outro fator que influi na dilatação linear de uma barra.

·        3º a variação de comprimento DL depende também do material de que é feita a barra (a ). O valor de a é uma característica de cada material mas não é rigorosamente constante com a temperatura. Costuma-se usar um valor médio de a entre as temperaturas usuais.

     Unidades de a : A unidade a é o inverso da unidade de temperatura.

                                1/ ºC    ou  ºC^-1

                                1/ ºF     ou  ºF^-1

                                1/ K      ou   K^-1

 Significado físico de a:

O coeficiente de dilatação linear representa a variação de comprimento unitário quando a temperatura varia de uma unidade.

Considere por exemplo, o coeficiente de dilatação linear do ferro que é 1,2 .10 ºC ^-1 , este número significa que, se tomarmos uma barra de ferro com um metro de comprimento e elevarmos sua temperatura em 1ºC, seu comprimento será 1,000012m.

  

 

Tabela de coeficientes de dilatação linear (a) de algumas substâncias:

Substância	Coeficiente  ºC-1	Substancia	Coeficiente ºC-1
Alumínio	24.10-6	Latão	18.10-6
Cobre	17.10-6	Níquel	13.10-6
Chumbo	29.10-6	Zinco	27.10-6
Aço	12.10-6	Platina	9.10-6
Ferro	12.10-6	Ouro	14.10-6
Prata	19.10-6	Vidro Comum	9.10-6
Mercúrio	41.10-6	Vidro Pirex	3.10-6

Nota: Lembrando que   DL = L_f- Li ,podemos também escrever

                      Lf - Li = a Li .  DT, isolando L, temos:

                      Lf = Li + a.Li. DT , colocando Li, em evidência, obtem-se:

                      Lf = Li( 1 + a. DT )

                   

                      Lf = Li [ 1 + a( Tf- Ti )]

Lembre que:    Ti - temperatura inicial

                          Tf - temperatura final

                          DT - variação de temperatura

                          DT = Tf - Ti

                           Li - comprimento inicial

                            Lf - comprimento final

        

                          DL - variação de comprimento

Exemplos:

1º) Uma viga de concreto (a = 12.10^-6 ºC ^-1)  tem 100m de comprimento a 20ºC. Que comprimento terá a viga a 30ºC?

                                                 

Exercícios de aplicação:

1)Qual será a dilatação sofrida por uma barra de ouro ( a = 15.10^-6  ºC^-1  ) inicialmente  de  comprimento 40 cm , quando a temperatura passa de 15ºC  para 35ºC ?

2)Um  sarrafo de madeira (a = 5.10^-6  ºC^-1 ) tem comprimento de  10m a 20ºC. Que comprimento terá a  70ºC.

3)Uma ponte de aço tem 1000m de comprimento. O coeficiente de dilatação linear do aço é de 11.10 ^-6    ºC ^-1 . A expansão da ponte, quando a temperatura sobe de 0ºC para 30ºC, é de:

a)33cm        b)37cm       c) 41cm        d) 52cm        e) 99cm

4)Duas barras metálicas são aquecidas sofrendo a mesma variação de temperatura. Qual delas apresentará a maior dilatação linear considerando que:

a)tenham o mesmo comprimento inicial.

b)sejam feitas do mesmo material.

c)sejam de materiais diferentes e tenham comprimentos iniciais diferentes.

5)Por que se costuma deixar um espaçamento entre dois trilhos; consecutivos de uma ferrovia?

6)O que significa fisicamente dizer que o coeficiente de dilatação linear de certo material vale 17.10  ^-6  ºC^-1   ?

7)A 10ºC, uma régua de aço mede 15cm. Qual será seu comprimento na temperatura de 80ºC?

8)O comprimento de um fio de alumínio é de 30m a 20ºC. Sabendo-se que o fio é aquecido até 60ºC e que o coeficiente de dilatação linear do alumínio é de 24. 10^{- 6} ºC^-1, determine:

a) a dilatação do fio;

b)o comprimento final do fio.

9)O comprimento inicial de uma barra de alumínio é de 100 cm . Quando sofre variação de 20ºC e sua dilatação é de 0,048 cm. Determinar o coeficiente de dilatação linear do alumínio.

10)Um trilho de aço tem 10m de comprimento a – 10ºC. supondo que a temperatura suba para 40ºC e que o coeficiente de dilatação do aço seja exatamente 12 . 10^{- 6} ºC^-1, determine:

a)o acréscimo de comprimento do trilho;

b)o comprimento final do trilho.

2.3-DILATAÇÃO SUPERFICIAL

     Consideremos uma chapa que apresenta uma superfície inicial So a uma temperatura inicial Ti. Ao aquecermos a chapa até uma temperatura final Tf, sua superfície aumenta para  Sf

          

   onde:

 Si - superfície  inicial    Sf- superfície final     DT - variação de temperatura

Ti - temperatura inicial    Tf- temperatura final   DS - variação de superfície

         DT = Tf - Ti                     DS = Sf - Si

Verifica-se experimentalmente que a variação da superfície é diretamente proporcional à superfície inicial e à variação da temperatura. Portanto:

                                                              

                                                                  DS = b. Si. DT

    

   A constante de proporcionalidade b, característica  do material da chapa, é chamada de coeficiente de dilatação superficial.

                                                                       b = 2. a

   Significado físico de b : O coeficiente de dilatação superficial b representa a variação de uma superfície unitária quando a temperatura varia de uma unidade.

   NOTA: Lembrando que  D S = Sf - Si, podemos também escrever:

                                           Sf -Si = b . Si . DT, isolando Sf temos:

                                           Sf = Soi+ b.Si.DT, colocando Si em evidencia, obtem-se

                                           Sf = Si( 1+ b.DT )  mas  DT = Tf - Ti

                                       

                                            Sf = Si [ 1 +b.( Tf - Ti) ]

EXEMPLO:

  Uma placa de ferro apresenta, a 10ºC, uma área de 100cm². Calcule a área  da placa a 90ºC . Dado :aFe  = 1,2.10^-6   ºC. ^-1

Exercícios de aplicação:

11)Uma placa metálica tem área de 500cm² a 30ºC. Qual será a área da placa a 50ºC? Dado: a = 2.10^{- 6} ºC^-1

12)Aquecendo-se uma chapa metálica com um furo no meio

a)a chapa aumenta e o furo diminui

b)a chapa e o furo diminuem

c)a chapa diminui e o furo aumenta

d)a chapa e o furo aumentam

13)Uma chapa de aço tem área de 36 m² a 30ºC. Calcule sua área a 50ºC, sabendo que o coeficiente de dilatação superficial do aço é 22 . 10^{- 6} ºC^-1 .

14) Determine a temperatura na qual uma chapa de cobre de área 10 m² a 20ºC assume o valor de 10,0056 m². Considere o coeficiente de dilatação superficial do cobre igual    a 34. 10^{- 6} ºC^-1

15)Uma chapa apresenta a 0ºC, 2 m² de área. Ao ser aquecida a 50ºC, sua  área  aumenta  10 cm² . Determine o coeficiente de dilatação superficial e linear do material de que é feita a chapa.

16) Uma placa de ferro apresenta, a 90ºC, uma área de 100,192 cm² . Calcule a área da placa a 10ºC

2.4 - DILATAÇÃO VOLUMÉTRICA

     Da mesma forma que na dilatação linear e superficial, na dilatação volumétrica a variação de volume é diretamente proporcional ao volume inicial (Vi) e à variação de temperatura.

       DT = Tf - Ti

       DV = Vf - Vi                                     DV = g.Vi. DT

     

   A constante de proporcionalidade g, é a característica do material de que é feito o corpo, chama-se coeficiente de dilatação volumétrica.  g = 3. a

   Significado físico de g: o coeficiente de dilatação volumétrica representa a variação de volume de uma unidade de volume, quando a temperatura varia de uma unidade.

EXEMPLO:

 Um tubo de vidro  tem volume de 500cm³ a 20ºC. Determine o volume interno desse tubo quando a temperatura  atingir 60ºC. Dado a vidro= 3.10 ^-6  ºC^-1 .

Exercícios de aplicação:

17) Um cubo metálico tem volume 20 cm ³à temperatura de 15ºC. Determine o seu volume à temperatura de 25ºC, sendo o coeficiente de dilatação linear do metal igual 0,000022ºC-¹

18)Qual será a dilatação volumétrica sofrida por uma esfera   metálica de alumínio de volume igual a 150 cm ³cuja temperatura aumenta de 100ºC? Dado a = 22.10^-6  ºC^-1

19)Uma esfera de aço tem um volume de 100cm³ a 0ºC. sabendo que o coeficiente de dilatação linear do aço é de 12.10^-6  ºC ^-1, o acréscimo de volume sofrido por essa esfera, quando aquecida a 500ºC, em cm é de:

a)0,6        b)1,2       c)1,8        d)3,6        e)5,0

20) Um caminhão tanque com capacidade para 10 000 litros está cheio de gasolina quando a temperatura é de 30ºC. Qual a redução de volume sofrida pelo líquido ao ser descarregado numa ocasião em que a temperatura é de 10ºC? O coeficiente de dilatação volumétrica da gasolina é g = 9,6 . 10 ^-4 ºC^-1.

5-DILATAÇÃO DOS LIQUIDOS

    Como os líquidos não apresentam forma própria, só tem significado o estudo de sua dilatação volumétrica.

     Ao se estudar a dilatação dos líquidos, tem de se levar em conta a dilatação do recipiente sólido que o contém.

     De uma maneira geral, os líquidos dilatam-se mais que os sólidos ao serem igualmente aquecidos.

 O líquido irá, ao dilatar-se juntamente com o recipiente, ocupar parte da dilatação sofrida pelo recipiente, além de mostrar dilatação própria, chamada dilatação aparente.

   A dilatação real do liquido é obtida pela soma da dilatação aparente apresentada diretamente pelo líquido mais a dilatação volumétrica sofrida pelo recipiente

                          

                        DV real = DVap +DV recip.

  

      Mas:     DVreal = greal.Vi.DT

                    DVap = gap. Vi . DT

                    DV recip.= grecip. Vi.DT

 Relação entre os coeficientes de dilatação real e aparente do líquido

                                                                                   greal = gap + grecip  

 6- DILATAÇÃO ANÔMALA DA ÁGUA

As substâncias em geral, solidas ou liquidas, sofrem dilatação com o aumento da temperatura e naturalmente, sofrem contração com sua diminuição. Porém, existem exceções a essa regra. Algumas substâncias, em certas faixas de temperatura, diminuem o volume ao serem aquecidas.

Dentre essas exceções destaca-se a água, que, ao ser aquecida de 0º a 4ºC, sofre diminuição em seu volume. É devido a esse fenômeno que as camadas mais profundas  dos lagos e mares podem estar a 4ºC e não se congelar como ocorre com suas superfícies. Na superfície dos lagos a água esfria primeiro, diminuindo de volume. Com isso torna-se mais densa, indo para o fundo. A água do fundo, mais quente, está menos densa e sobe à superfície, onde é resfriada. Quando toda a água está a 4ºC, cessa a circulação. Se a temperatura da superfície cai abaixo de 4ºc, a água vai tornar-se menos densa; permanecerá, então, na superfície, podendo solidificar-se e formar camadas de gelo a 0ºC.

   Se a água não apresentasse esta irregularidade na dilatação, os rios e lagos se congelariam totalmente, causando estragos às plantas e animais aquáticos.

EXEMPLO:

Um recipiente contém 200 cm ³ de mercúrio a 10ºC. Sabendo-se que os coeficientes de dilatação volumétrica do vidro e do mercúrio são respectivamente 0,00003 ºC ^–1 e 0,00018 ºC ^–1  , determine a dilatação real e a dilatação aparente do mercúrio, quando a temperatura for 120ºC

Exercícios de aplicação:

21)Um frasco de vidro, cujo volume é 300 cm ³ a 10ºC, está completamente cheio de um certo líquido. Quando se aquece o conjunto a uma temperatura de 140ºC, transbordam 2 cm ³ do liquido. Sendo o coeficiente de dilatação volumétrica do frasco igual a  0,00027   ºC ^–1, determine:

a)     o coeficiente de dilatação volumétrica aparente do líquido,

b)    o coeficiente de dilatação volumétrica real do líquido.

22)Um recipiente de vidro contém 400 cm ³ de mercúrio a 20ºC. Determine a dilatação aparente do mercúrio, quando a temperatura for 90ºC. Dados:gHg = 0,00018ºC ^–1    e   gvidro=0,00003  ºC ^–1                                                                                      

23)O que se entende por dilatação aparente de um líquido?

24)Um frasco, completamente cheio de um líquido, é aquecido e transborda. O volume de líquido que transborda mede:

                            (   )a dilatação real do líquido

                            (   )a dilatação aparente do líquido

                            (   )a dilatação do frasco

25)Nos países de inverno rigoroso, verifica-se o congelamento  apenas da superfície dos lagos e rios. A água não se congela completamente porque:

a)o máximo de densidade da água se verifica perto de 4ºC e o gelo, razoável isolante térmico, é menos denso que a água.

b)o ar se resfria antes da água, congelando-se primeiro a superfície dos líquidos em contato com o referido ar e, daí, propagando-se o congelamento em profundidade.

c)a água em movimento dificilmente se congela

d)a água se comporta como a maioria dos líquidos em relação ás variações de temperatura

e)n.d.a